How to calculate volume
Volume forms one of the base variables in geometry, which defines the measure of space that a three-dimensional object occupies. Calculating volume plays an important role in filling in containers, product design, or solving mathematical problems.
This is simply because it helps us quantify the space that an object occupies in three-dimensional space. Thus, it would allow us to estimate the capacities and quantities of materials required, among others.
To determine the volumes of different shapes, you will need to use different formulas based on their geometrical properties. The volume of some regular shapes, such as a cylinder, cube, sphere, rectangular prism, cone, and pyramid, is defined by a specific mathematical formula describing the occupation of space.
Today, we are going to explain, step by step, how to calculate the volume for each one of those shapes using practical examples. First, however, let’s define what volume is and what common units of volume are.
Course of Content:
- What is Volume?
- How to Calculate the Volume of a Cylinder
- How to Calculate the Volume of a Cube
- How to Calculate the Volume of a Sphere
- How to Calculate the Volume of a Rectangular Prism
- How to Calculate the Volume of a Cone
- How to Calculate the Volume of a Pyramid
- How to Calculate Volume of a Torus (Donut Shape)
- Common Mistakes to Avoid When Calculating Volume
What is Volume?
Volume measures the total space an object or fluid occupies in terms of a container. It is, in fact, a measure of how much space is inside something, how much substance there is in a given structure, or how much of a substance can be contained in it. It is part of geometry definitions and is used significantly in the sciences, engineering, architecture, and almost every other phase of living.
In the simplest metric terms, volume is almost always measured in cubic terms such as cubic meters, cubic centimeters, or liters, depending on the measuring system in use. For instance, when measuring a box to find out its volume, what we are really looking for is how much space is available in the box.
Key Concepts of Volume:
- Three-Dimensional Measurement: The volume, unlike area that shows the surface of a shape (two-dimensional), tells how much space an object occupies in all three dimensions: length, width, and height or depth.
- Formula-Based: The volume of an object is shape-dependent, meaning different geometric shapes provide for different formulas to reach its volume. Most formulas are based on parameters – object dimensions, length-width-height – and constants: π (for circular shapes).
- Practical Importance: The volume finds its application in quite a wide range; from how much liquid a vessel can hold to the determination of space inside buildings or storage facilities.
Units of Volume and Conversion Between Units
Different systems of measurement have different units for expressing volume. They include cubic meters, liters, and gallons, among others. Conversion between these units is, therefore, crucial in solving problems that might involve different contexts.
Common Units of Volume:
- The metric system includes the following units:
- Cubic meters (m³): It is the SI unit of measurement for volume.
- Liters (L): It is usually used to measure the volume of liquids
- Cubic centimetre: Normally used in scientific contexts where 1cm³ = 1 ml.
- Common units in the imperial system include
- Cubic inches (in³) and Cubic feet (ft³) and gallons
Conversion Factors:

These units are necessary when it comes to conversions. For example:
How many Liters do you think 2 cubic meters is?
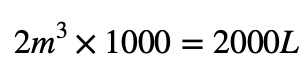
So, two cubic meters equals 2000 liters.
How to Calculate the Volume of a Cylinder

A cylinder is a three-dimensional figure that is made of two parallel circles co-axial with each other and joined by a curved surface. The space between the two bases is the height of the cylinder. Cylinders are used in cans, pipes, and some of the batteries which are used in our daily lives.
To calculate the volume of a cylinder, you need two key measurements:
- Radius (r) of the circular base (the distance from the center of the base to its edge).
- Height (h) of the cylinder (the distance between the two circular bases).
The formula for the volume of a cylinder is:
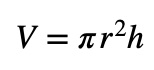
This formula is derived from the understanding that the area of the circular base is πr2 and then multiply it by its height to have the total volume of the cylinder.
Here is an Example:
Imagine you’re designing a cylindrical water tank with a radius of 7 meters and a height of 10 meters. To find the volume of water the tank can hold:
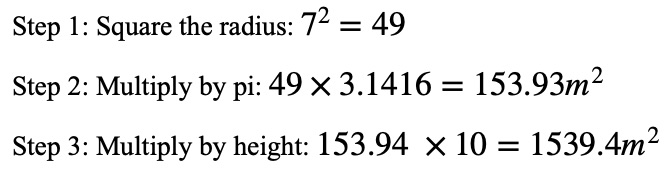
So, the volume of the tank is 1539.4 cubic meters. This volume represents the total capacity of the tank.
How to Calculate the Volume of a Cube

A cube is a rectangular prism in which all the sides have the same measurement, therefore having equal length, breadth, and height. All its faces are squares, and all its edges are equal. This shape is present in dice, boxes, and several packaging structures across different industries.
The formula for the volume of a cube is simple:
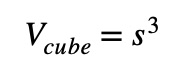
Here, s stands for measurement of each side of a cube respectively. Since the edges of a cube are congruent, the process of finding volume is quite simple, and this is by cubing the side.
Example:
Let’s assume you have a cube-shaped gift box whose one side measurement is 6 inches. Therefore, the volume for this cube will be:
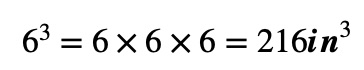
This means that the box can accommodate other objects whose volume has to be not more than 216 cubic inches in total.
How to Calculate the Volume of a Sphere
A sphere is a perfectly symmetrical structure in equidistance dimensional geometry in which each point on the shell is at an equal distance from the shell’s center. Things that are similar to spheres are balls like basketballs, celestial bodies like planets, and even bubbles.
The variables used in the sphere volume formula are r, the distance from the center of the sphere to its surface. The formula for the volume of a sphere is:
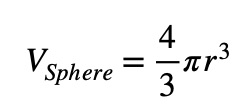
Hence, this formula originated from calculus, whereby the sphere has an infinite continuous curvature.
The 4⁄3 factor takes care of all the curvature in all directions.
Real-Life Example:
If you’re calculating the volume of a ball with a radius of 5 cm:
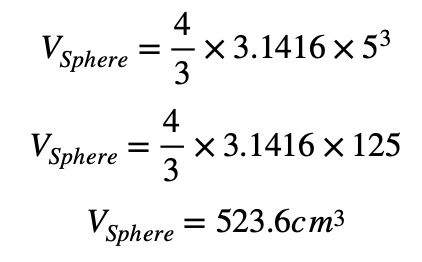
Thus, the volume of the ball is 523.6 cubic centimeters.
How to Calculate the Volume of a Rectangular Prism
A cuboid is a three-dimensional shape called a rectangular prism by some since it has six rectangular flat faces. The dimensions of a rectangular prism are the length, width and height of the rectangular prism. A rectangular prism is simply a rectangular shaped solid that is often used to represent such everyday objects as boxes for shipment and storage or furniture items.
To calculate the volume of a rectangular prism, you multiply the three dimensions together:
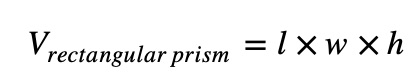
This formula is effective since volume is equal to the base, which is the product of length ×\times×width and the height.
Real-Life Example:
If you’re measuring a bookshelf that is 80 cm long, 30 cm wide, and 150 cm tall:
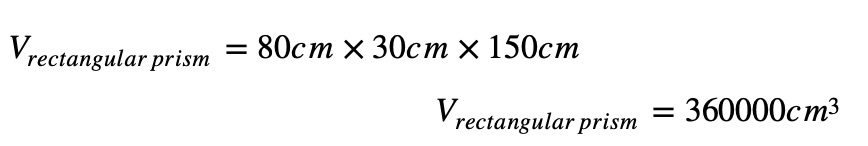
Hence, the volume of the bookshelf is 360000 cm³. If you need liters, you will need to convert it by simply dividing by 1000 cm³ (since 1 liter = 1000 cm³), equaling 360 liters. This volume indicates the space occupied by the bookshelf.
Related: Prism Surface Area Calculator
How to Calculate the Volume of a Cone
A cone is another three dimensional figure having a circular plane at the base and one point at the top. The volume of a cone is, in fact, one-third that of a cylinder that has the same base and height. Cone examples are ice cream cones, traffic cones, and some of the funnels used in laboratories.
To calculate the volume of a cone, use the following formula:
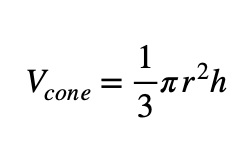
This formula works by having the base in the shape of a circle, which is represented by . Then, multiply it by the height and divide the lot by three because the cone gradually fades to a point.
Real-Life Example:
Suppose you have an ice cream cone with a radius of 3 cm and a height of 12 cm:
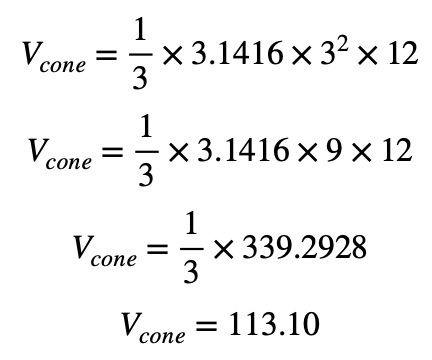
Thus, the volume of the ice cream cone is 113.10 cubic centimeters. This volume represents how much ice cream the cone can hold.
How to Calculate the Volume of a Pyramid
A pyramid is one of the 3D shapes that is made up of a polygon base and triangles of faces that connect at a main point known as the apex. The base of most pyramids is square, but a pyramid can be made of any polygon. Pyramids’ volume is 1/3 of the product of the base and the height of the pyramid.
To calculate the volume of a pyramid, the formula is:
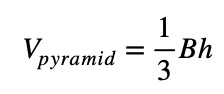
Where:
- B represents the area of the base (for a square base, B = S^2 )
- h is the height of the pyramid, measured from the center of the base to the apex.
Real-Life Example:
If you have a square pyramid with a base side length of 6 meters and a height of 10 meters:

So, the volume of the pyramid is 120 cubic meters. This is how much space the pyramid occupies.
How to Calculate Volume of a Torus (Donut Shape)
A torus is a doughnut-shaped 3D object, which, in other words, can be described as the product of revolving a circle in space. It’s commonly used in engineering and design.
The formula for the Volume of a Torus:
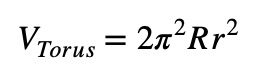
Where:
- R is the radial distance, which is the distance between the center of the hole and the center of the tube.
- r is the radius of the tube itself.
Example:
Consider a torus with an outer radius R = 10 cm and an inner tube radius r = 2 cm.
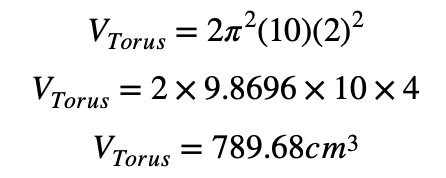
So, the volume of the torus is approximately 789.68 cubic centimeters.
Volume of a Hollow Object (Shell Method)
An object, for instance, a pipe or a hollow sphere, has the outer and inner volume of that object. The volume of the hollow part is calculated by the difference in the outer volume from the inner volume.
Formula:
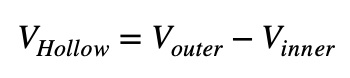
Example (Hollow Cylinder):
If a hollow pipe has an outer radius of 5 cm, an inner radius of 4 cm, and a height of 10 cm:
So, let’s start by calculating the volume for the outer circle:
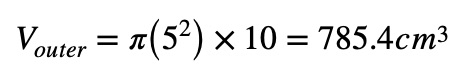
No, let’s go for the inner circle:
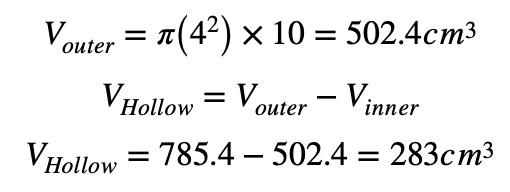
So, the volume of the hollow section is 283 cubic centimeters.
How to Calculate Volume of a Prism with Non-Rectangular Bases
Prisms can have polygonal bases other than rectangles, such as triangles or hexagons. The formula remains the same, but the base area (BBB) must be calculated based on the specific polygon.
The formula for the Volume of a Prism:
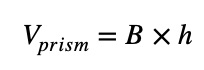
Example (Triangular Prism):
For a triangular prism with a base triangle area of 20 cm² and a height of 15 cm:
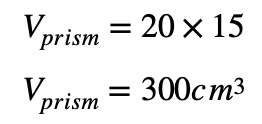
So, the volume of the triangular prism is 300 cubic centimeters.
Relationship Between Surface Area and Volume
While the surface area and volume of an object seem similar, they behave in different ways when size is concerned. Scaling an object by twice its size does not mean that its volume has doubled; it is much more than that.
Example (Cube):
If a cube has a side length of 2 meters:
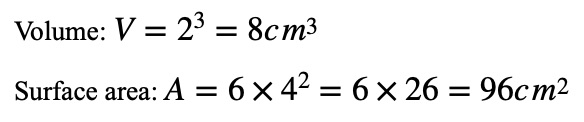
If the side length is doubled to 4 meters:
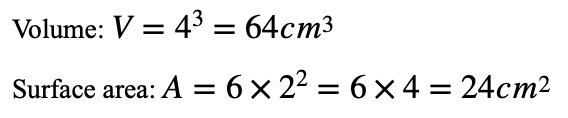
Doubling the side length increased the volume by a factor of 8, but the surface area increased by a factor of 4.
How to Calculate Volume Using Integration (Advanced Topic)
Calculus provides tools like integration to calculate volume for complex shapes where standard volume formulas don’t apply. This method involves slicing the object into infinitely thin cross-sections and summing their areas.
The formula for Volume by Integration (Revolved Around the x-axis):
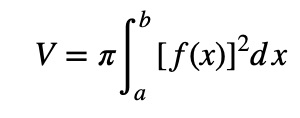
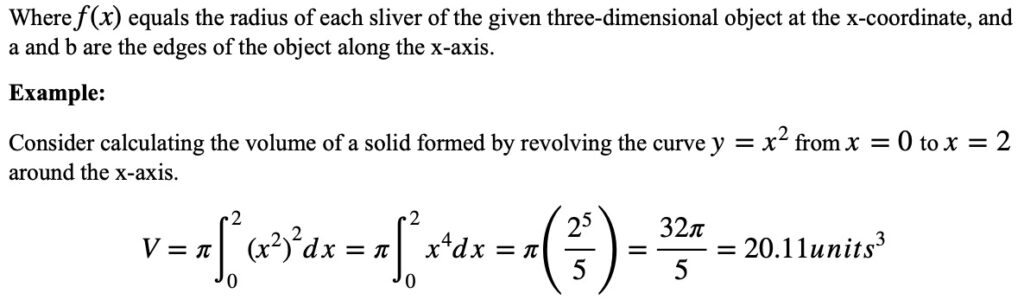
So, the volume of the solid is approximately 20.11 cubic units.
Common Mistakes to Avoid When Calculating Volume
It is easy to think that calculating volume is quite simple, but there are a number of pitfalls that can cause mistakes to be made. Here are some of the most frequent errors and how to avoid them:
- Using Incorrect Units
Volume calculations include measurements in different units, which may be in cm, m, or inches. Probably the most frequent error is the usage of improper units or the lack of correct unit conversions.
2. Forgetting to Cube the Units
When calculating volume, you have to multiply the linear measurements, that is, length, width, height, or radius, by their cube. One should not forget that the extra value at the end of the expression must be cubed while working on more complicated expressions with powers or fractions.
3. Misapplying the Volume Formula
Some of the problems that arise when applying the volume formula include the following Misapplication of the volume formula.
Every geometrical shape has its unique method of calculation of volume. One pitfall is using the wrong formula or using the formula of two similar shapes, such as a cone and a cylinder or a pyramid and a rectangular prism.
4. The Misinterpretation of the Dimensions
At times, it becomes difficult to distinguish between heights, radii, and diameters of the objects or even shapes that are not standard. If an individual decides to use the wrong dimension in a formula, he or she will end up with a wrong answer.
5. Confusing Between the Height and Slant Height of Cones and Pyramids
Cylinders and spheres, on the other hand, may have a slant height (the length of the side from the top to the base) and a regular height (the distance from the top to the base). When finding the volume, one pitfall is mistaking the slant height for the perpendicular height.
Conclusion
The measurement of the volume of different three-dimensional figures is essential in real-life situations, from the development of containers and packaging to the construction of buildings and different objects.
Because each of these shapes has a specific formula, it is possible to calculate the volume of most of the everyday objects.
Every shape has its formula, which depends on the properties of the geometric figure, but all of them presuppose the multiplication of the base area by the height or radius and the addition of the necessary constants (such as π or 1⁄3) for rounding or narrowing the figure.

















