How to Calculate Percentage

In everyday circumstances and in a range of areas of study, such as business, finance, and education, percentage calculations are important. Percentages provide a quick approach to express proportions and changes, whether you’re calculating discounts, comparing growth rates, or figuring out grade improvements.

We’re going to help you through the process of calculating percentages in this article, presenting the formulas and important topics using examples from everyday life.

This guide will delve into various types of percentage calculation, including:

• How to Calculate Percentage of a Number
• How to Calculate the Percentage Change
• How to Calculate Percentage Difference
• How to Calculate Percentage Increase
• How to Calculate Percentage Decrease
• Percentages in Probability and Statistics
• Percentages in Business and Marketing
• Percentages in Health and Fitness
• Percentages in Environmental Science
• Percentages in Psychology and Behavioral Science
  

How to Calculate Percentage of a Number

To calculate the percentage of a number, you multiply the number by the percentage and divide by 100. This simple calculation can help you find proportions, such as how much of a budget is spent on different categories or the percentage of correct answers on a test.

Formula

𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 𝑜𝑓 𝑎 𝑛𝑢𝑚𝑏𝑒𝑟 = ( 𝑝𝑎𝑟𝑡 / whole ) × 100

Example

1. If you want to find what 30% of 60 is:

𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 = ( 30 / 100 ) × 60 = 18

Thus, 30% of 60 is 18.

2. If you want to calculate 15% of $200 is:

𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 = ( 15 / 100 ) × 200 = 30

Thus, 15% of 200 is 30.

3. If you scored 80 points out of 100 on a test and want to know the percentage score:

𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 = ( 80 / 100 ) × 100 = 80%

You scored 80% on the test.

Explanation

In example number 1, first of all you convert the percentage into a fraction form, like 30% when we write in fraction, It will be a (30 / 100) . After this one, you will multiply a number that you want to find a percentage like 60.

Then you simplify it, and you will get the solution, that is 18 for this example. This calculation helps you determine a part of a whole based on a percentage.

Real-Life Applications

• Sales Tax: If an item costs $100 and the sales tax is 8%, you can calculate the tax amount by multiplying $100 by 8%, which gives $8 in tax.
• Tip Calculation: To tip 20% on a $50 bill, you multiply $50 by 20% ($50 × 0.20), which equals $10.

By learning this method, you can easily handle real-life calculations like discounts, tips, and taxes.

Related: Percentage calculator

How to Calculate the Percentage Change

Percentage change is used to show the difference between an old and a new value, expressed as a percentage of the old value.

This calculation is common in analyzing data trends, such as the change in stock prices, revenue growth, or population shifts.

Formula

𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 𝐶h𝑎𝑛𝑔𝑒 = ((𝑁𝑒𝑤 𝑣𝑎𝑙𝑢𝑒 − 𝑂𝑙𝑑 𝑣𝑎𝑙𝑢𝑒) / Old Value) / × 100

Example

1. If a company’s revenue grew from $200,000 to $260,000, the percentage change in revenue is:

𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 𝐶h𝑎𝑛𝑔𝑒 = ((260,000 − 200,000) / 200,000) × 100

= ( 60,000 / 200,000 ) × 100

= 30%

So, the revenue increased by 30%.

2. If your savings grew from $1,000 to $1,200, you can calculate the percentage change as:

𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 𝐶h𝑎𝑛𝑔𝑒 = ((1200 − 1000) / 1000) × 100

= 20%

So, your savings increased by 20%.

3. If the stock price of a company decreased from $150 to $120, the percentage change is:

𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 𝐶h𝑎𝑛𝑔𝑒 = ((120 − 150) / 150) × 100

= −20%

The stock price dropped by 20%.

Explanation

We subtract the old value from the new value to find the absolute change and then divide it by the old value to find the relative change. Multiplying by 100 converts the result to a percentage.

Applications of Percentage Change

• Financial Growth: Investors use percentage change to track stock price movements, investment growth, or revenue changes.
• Inflation Rates: Economists measure inflation by comparing the change in the price index of goods and services over time.
• Performance Tracking: Businesses use percentage change to measure key performance metrics like sales growth, customer acquisition, or website traffic.

How to Calculate Percentage Difference

Percentage difference is used to compare two values that are not directly related, showing the relative difference as a percentage of the average of the two values. This method is useful for comparing performance, measurements, or prices.

Formula

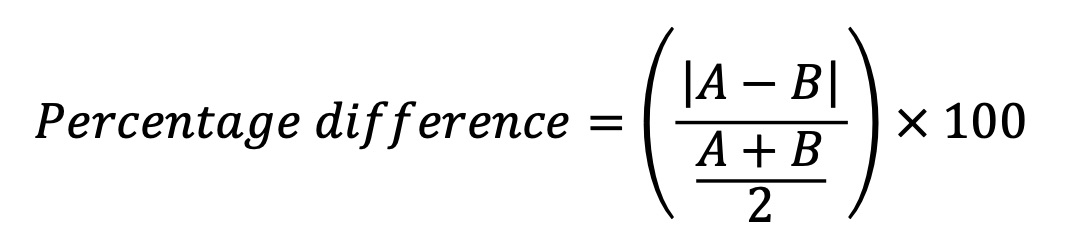
Example

If one product costs $30 and another costs $60, the percentage difference between the prices is:

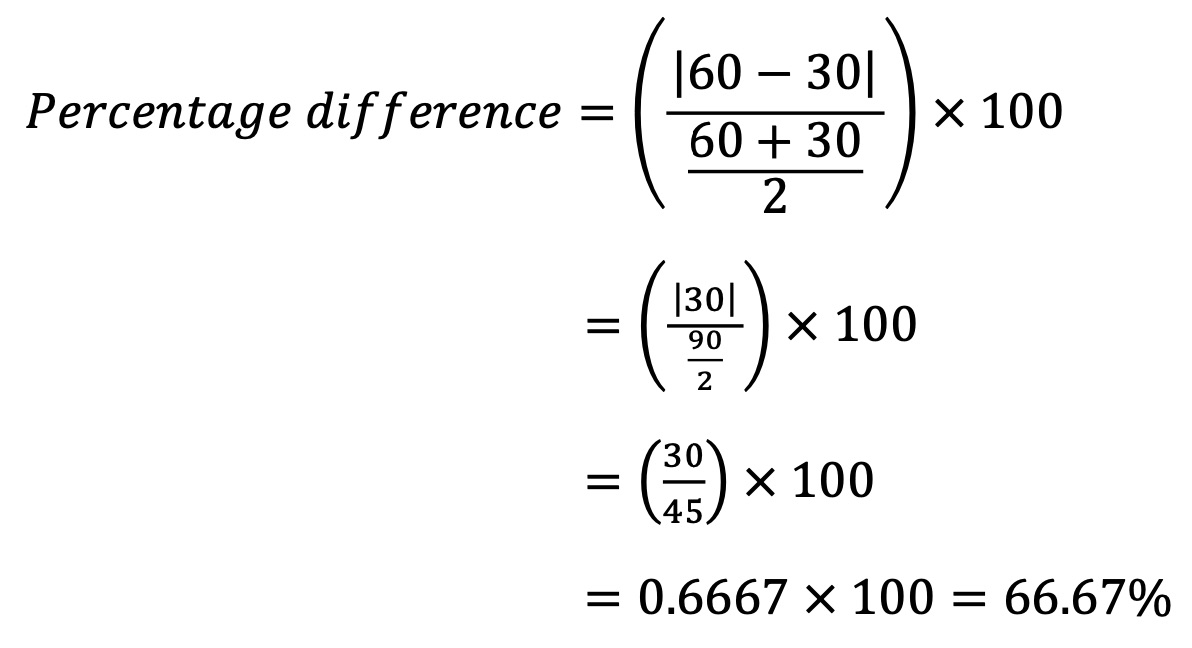
Thus, the price difference between the two products is about 66.67%.

Explanation

Here, the absolute difference between the two values is divided by their average to provide a relative comparison in percentage terms. This formula is particularly useful when comparing values that are not based on a single reference point.

Applications of Percentage Difference

• Comparing Product Prices: Consumers often compare prices of similar products to find the best value, and percentage difference helps quantify these comparisons.
• Quality and Performance: Manufacturers may use percentage difference to compare the performance or durability of two products, helping to determine which is more efficient or cost-effective.

How to Calculate Percentage Increase

Percentage increase refers to how much a quantity has increased compared to its initial value. This calculation is widely used in finance, sales, and performance tracking.

Formula

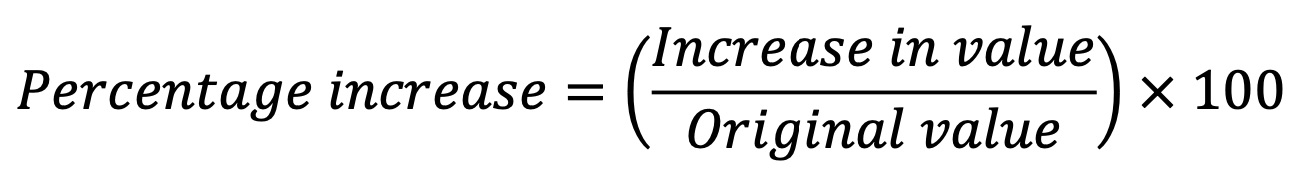
Example

1. If your salary increased from $5,000 to $5,500, the percentage increase is:

𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 𝑖𝑛𝑐𝑟𝑒𝑎𝑠𝑒 = ( 500 / 5,000 ) × 100

= 10%

So, your salary increased by 10%.

2. If a shop’s monthly sales increase from $2,000 to $3,000,

the percentage increase is:

𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 𝑖𝑛𝑐𝑟𝑒𝑎𝑠𝑒 = ( 1000 / 2,000 ) × 100

= 50%

So, the sales grew by 50%.

Explanation

We calculate the increase (difference between the new and original values) and divide it by the original value to determine the proportion of increase. The result is multiplied by 100 to get the percentage.

Applications of Percentage Increase

• Salary Growth: Employees calculate the percentage increase in their salary after a raise to determine how much their earnings have improved.
• Business Growth: Companies track revenue or sales growth using percentage increase to measure performance over time.
• Price Increases: Consumers often calculate the percentage increase in product prices to determine whether a price hike is significant.

How to Calculate Percentage Decrease

Percentage decrease is the opposite of percentage increase and indicates how much a value has fallen compared to its original amount. It is often used in situations like calculating price drops, budget cuts, or declines in performance metrics.

Formula

Percentage decrease = (Decrease in value / Original value ) x 100

Example

If the price of an item was reduced from $60 to $30, the percentage decrease is:

𝑃𝑒𝑟𝑐𝑒𝑛𝑡𝑎𝑔𝑒 𝑑𝑒𝑐𝑟𝑒𝑎𝑠𝑒 = (30 / 60) × 100

= (300 / 6)

= 50%

Thus, the price decreased by 50%.

Explanation

In this case, the difference between the original and new values represents the decrease. Dividing by the original value and multiplying by 100 gives the percentage of the decrease.

Applications of Percentage Decrease

• Discounts: Shoppers calculate percentage decreases during sales to determine how much they’ve saved on a purchase.
• Cost Cutting: Businesses use percentage decrease to track reductions in operational costs or expenses over time.
• Environmental Data: Analysts may calculate the percentage decrease in pollution levels or energy usage as part of sustainability efforts.

Percentages in Probability and Statistics

Percentages play a key role in probability and statistics, helping to express likelihoods and distributions in an easy-to-understand format. Whether it’s the probability of an event happening or a breakdown of a dataset, percentages make statistical data accessible.

Probability as a percentage

In probability theory, the likelihood of an event occurring can be expressed as a fraction, decimal, or percentage. Using percentages makes it easier for most people to grasp the concept of chance.

Formula for Probability as a Percentage

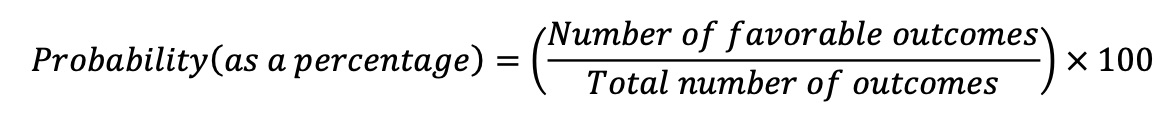
Example

If you roll a fair six-sided die, the probability of rolling a 3 is:

𝑃𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦 = (1 / 6) × 100 = 16.67%

So, there’s a 16.67% chance of rolling a 3.

Explanation

Expressing probability as a percentage allows you to communicate the likelihood of events in simple, relatable terms. Percentages are often used in this way in sports statistics, weather forecasts, and risk analysis.

Percentages in data distribution

In statistics, percentages are used to express how data is distributed across categories or ranges. For example, a company might want to know what percentage of their customers fall into different age groups or income brackets.

Example

If a survey shows that 200 out of 1,000 respondents prefer Product A, the percentage of customers who prefer Product A is:

(200 / 100) × 100 = 20%

Data is often presented in pie charts or bar graphs, where each section represents a percentage of the whole. This helps in understanding the overall distribution and in comparing different categories effectively.

Percentages in Business and Marketing

Businesses frequently use percentages to measure performance, track progress, and make strategic decisions. Percentages help quantify everything from customer engagement to profit margins.

Conversion Rates

In digital marketing, conversion rate is a critical metric that measures the percentage of visitors who complete a desired action (such as making a purchase or signing up for a newsletter) on a website.

Formula for Conversion Rate

𝑪𝒐𝒏𝒗𝒆𝒓𝒔𝒊𝒐𝒏 𝑹𝒂𝒕𝒆 = (𝑵𝒖𝒎𝒃𝒆𝒓 𝒐𝒇 𝒄𝒐𝒏𝒗𝒆𝒓𝒔𝒊𝒐𝒏𝒔 / 𝑻𝒐𝒕𝒂𝒍 𝒏𝒖𝒎𝒃𝒆𝒓 𝒐𝒇 𝒗𝒊𝒔𝒊𝒕𝒐𝒓𝒔) × 100

Example

If 50 out of 1,000 website visitors make a purchase, the conversion rate is:

(50 / 1000) × 100 = 5%

So, the website has a conversion rate of 5%.

Explanation

Businesses use conversion rates to measure the effectiveness of their marketing efforts and website performance. A higher conversion rate indicates more successful marketing campaigns.

Profit Margins

Profit margin is another essential percentage used in business to measure the profitability of a company. It represents how much of the revenue is retained as profit after expenses are deducted.

Formula for Profit Margin

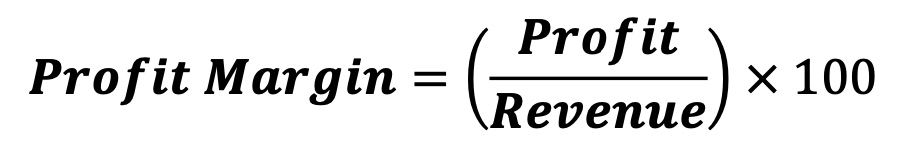
Example

If a business generates $10,000 in revenue and $7,500 in expenses, the profit is $2,500, and the profit margin is:

( 2500 / 10000 ) × 100 = 25%

The company has a profit margin of 25%.

Explanation

A high profit margin indicates that a company is running efficiently and effectively, while a lower margin might suggest the need to control costs or increase revenue.

Percentages in Health and Fitness

In the health and fitness industry, percentages are commonly used to measure body composition, caloric intake, and workout efficiency.

Body Fat Percentage:

Body fat percentage is the proportion of fat in your body compared to everything else (muscles, bones, water, etc.). This is an essential metric for understanding fitness levels.

Formula for Body Fat Percentage

𝑩𝒐𝒅𝒚 𝑭𝒂𝒕 𝑷𝒆𝒓𝒄𝒆𝒏𝒕𝒂𝒈𝒆 = ( 𝑻𝒐𝒕𝒂𝒍 𝑭𝒂𝒕 𝑴𝒂𝒔𝒔 / Total Body Weight) × 100

Example

If someone weighs 150 lbs and has 30 lbs of fat, their body fat percentage is:

( 30 / 150 ) × 100 = 20%

So, 20% of their body weight is fat.

Explanation

Body fat percentage is more important than weight alone when it comes to assessing fitness. It provides insight into the composition of your body, helping athletes and fitness enthusiasts optimize their training.

Caloric Breakdown

When analyzing your diet, percentages are used to understand how much of your daily caloric intake comes from carbohydrates, proteins, and fats.

Example

If your daily caloric intake is 2,000 calories and 800 of those come from carbohydrates, the percentage of calories from carbohydrates is:

( 800 / 2000 ) × 100 = 40%

Thus, 40% of your daily calories come from carbohydrates.

Explanation

This percentage breakdown helps individuals tailor their diet based on nutritional needs, whether for weight loss, muscle building, or maintaining a balanced diet.

Percentages in Environmental Science

Percentages are used extensively in environmental science to quantify data related to climate change, pollution, and resource consumption.

Carbon Footprint Reduction

As individuals and companies look to reduce their environmental impact, calculating the percentage reduction in carbon footprint can help measure success.

Formula for Percentage Reduction in Carbon Footprint

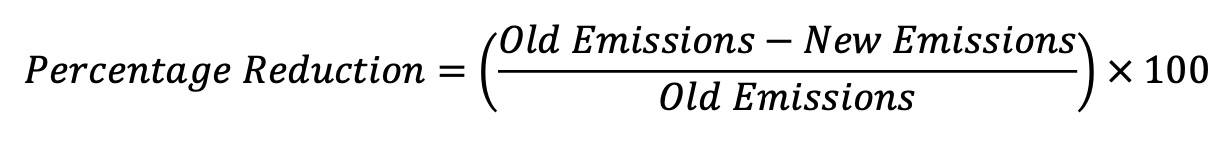
Example

If a company reduces its carbon emissions from 10,000 metric tons to 7,500 metric tons, the percentage reduction is:

((10,000 − 7,500) / 10,000) × 100 = 25%

So, the company has reduced its carbon footprint by 25%.

Explanation

As environmental sustainability becomes more critical, percentages help communicate progress in reducing emissions and energy consumption.

Renewable Energy Usage

Countries and companies track what percentage of their energy comes from renewable sources, such as solar, wind, and hydroelectric power, to measure progress toward sustainability goals.

Example

If a country’s total energy consumption is 1 million megawatt-hours, and 300,000 megawatt-hours come from renewable sources, the percentage of renewable energy usage is:

( 300,000 / 1,000,000 ) × 100 = 30%

Thus, 30% of the country’s energy comes from renewable sources.

Explanation

Tracking renewable energy usage as a percentage helps policymakers and companies set goals and evaluate the transition to cleaner energy solutions.

Percentages in Psychology and Behavioral Science

Percentages are often used in psychology and behavioral science to present research findings, including survey results, clinical trials, and psychological studies.

Survey Results and Polls

When psychologists conduct surveys or polls, they use percentages to represent the proportion of people who exhibit a particular behavior or express a specific opinion.

Example

If a survey asks 1,000 people whether they experience anxiety and 400 say yes, the percentage of people who experience anxiety is:

( 400 / 1,000 ) × 100 = 40%

This shows that 40% of respondents report experiencing anxiety.

Clinical Trails

In clinical research, percentages are used to express the effectiveness of treatments or interventions. For example, researchers might report the percentage of patients who experienced improvement in their condition after receiving treatment.

Example

If 200 out of 500 patients show improvement after taking a new medication, the percentage of patients who improved is:

(200 / 500) × 100 = 40%

Thus, 40% of the patients experienced improvement.

Explanation

Percentages in clinical trials help researchers convey the effectiveness of treatments and inform healthcare providers about the potential outcomes of different therapies.

Percentages in Voting and Elections

In democratic processes, percentages are used to determine the outcome of elections, referendums, and polls.

Voter Turnout

Voter turnout is often expressed as a percentage of eligible voters who participated in an election. This helps to understand how engaged the population is in the democratic process.

Example

If 10 million people are eligible to vote and 6 million actually cast a vote, the voter turnout percentage is:

( 𝟔, 𝟎𝟎𝟎, 𝟎𝟎𝟎 / 𝟏𝟎, 𝟎𝟎𝟎, 𝟎𝟎𝟎 ) × 100 = 60%

Explanation

Voter turnout percentages are important for understanding the level of public engagement and the legitimacy of the election results.

Election Results

Election results are commonly expressed in percentages to show how much of the vote each candidate or party received.

Example

If a candidate receives 3,000 votes out of a total of 10,000 votes, the percentage of votes they received is:

( 3,000 / 10,000 ) × 100 = 30%

Thus, the candidate received 30%

Conclusion

Mastering percentage calculations is a crucial skill, whether you’re dealing with financial data, academic scores, or everyday tasks like shopping discounts.

This guide covered essential percentage calculations, including how to calculate a percentage of a number, percentage change, percentage difference, percentage increase, and percentage decrease. Understanding and applying these formulas will help you make sense of data and comparisons in various aspects of life.

Whether you’re calculating your savings, determining a price discount, or tracking business growth, percentages allow you to express changes and comparisons effectively.

By practicing these calculations, you will strengthen your mathematical skills and be able to apply them confidently in various contexts.

Explore our different calculators