How to Calculate Average: Examples and Real-Life Applications
Do you know what an average sum of something is and how to calculate averages? If not, then don’t worry because, in this article, we will answer that, including other common mathematical calculations that you may need in your daily life.
It is worth noting that averages play a vital role in data analysis. As you may have noted, data analysis is virtually a common theme in nearly any field. Therefore, this means it is a valuable concept across many fields, including business, education, and healthcare.
Another valuable thing to note is that there are different types of averages. With these averages, you can easily simplify complex datasets by summarizing data, understanding trends, and making sound decisions. This guide will delve into various types of averages, including:
We will also give examples that will help illustrate their importance with real-life applications and detailed calculations.
What is the formula to calculate the average?
When dealing with several sets of numbers, you can use the average, which is the arithmetic mean, to find the central value of all those sets of numbers. This means that you can get a quick summary of a data set more so when the data points are evenly distributed.
Formula
Average = Σ Values / Number of Values
Importance: The average is useful when the dataset involves numbers all carrying equal importance, and there are no outliers that can skew the result. With that in mind, arithmetic calculation, therefore, can be used in everyday life, from the average speed of cars on road trips to summarizing test scores in education.
Real-Life Application (Example):

Let’s say you’re a maths teacher, and you want to determine the average performance based on these test scores: 75, 88, 92, 65, and 80. So, how do you go about it?
Well, it is simple; all you need to do is complete these two steps: Add all the values and then divide that by the number of values.
STEP 1: Add the values: 75 + 88 + 92+ 65 + 80 = 400
STEP 2: Divide by the number of scores (5):
Average = 400 / 5 = 80
And just like that, you can determine the average score for the class to be 80. This average is essential in determining and understanding the overall performance of the class.
Besides education, how is averages valuable, let’s say, for example, in business? Well, one of the metrics in business is what we call Kye performance indicators (KPI), and you can determine these using sales averages or any other data sets.
Example in Business:
Let’s say you have an online retail store, and you have made these sales in a week: $500, $700, $450, $600, $800, $750, and $650.
So, based on these numbers, what do you think is the average amount of money you can make on sales alone? To define this, you will need to complete the same steps as the one we’ve highlighted above: add and divide.
$500 + $700 + $450 + $600 + $800 + $750 + $650 = 4450
Average = 4450 / 7 = 635.71
From this calculation, we can tell that the store made average daily sales of $635.71 that week.
Why do we calculate averages?
When dealing with large data, it is hard to determine and represent that data with one single value. Therefore, to deal with that problem, averages are used to summarize data into a single representative figure. Other benefits of averages include:
- Simplifying complex datasets: For instance, in healthcare, they often determine the effectiveness of specific treatments by calculating their average recovery times. Another example is calculating student performance – Calculation below:
- Identifying trends: Averages are also calculated to show the direction of the movement of some process or phenomena over a specific period of time. For example, an employer can easily determine if employees are overworked by simply calculating their average working hours per week.
- Comparative analysis: Looking at sales or profits and other measures, most company averages will be equally useful in comparing the performance of specific branch sales, profits, and other measures within a given time period.
Example
Let’s say a student has the following scores in different subjects: 82, 91, 78, and 85 in four subjects. So, to calculate their average performance, we will have to:
- Add the scores: 82+91+78+85=336
- After finding the overall scores, we then divide that by the number of subjects, which in this case is 4:
Average = 336 / 4 = 84
The student’s average score is 84. This number helps teachers and parents understand how the student is performing across multiple subjects.
How to calculate the median?
When dealing with datasets that have outliers, averages don’t work well. Therefore, the median is particularly useful in datasets where outliers or extreme values may exist that could skew the average.
But what does median really refer to? It is about focusing on the middle data.
Focusing on the middle value within a dataset, the median gives a better indication of the middle point in those cases when the arithmetic mean may not be appropriate.
How to calculate the median:
Steps:
- Start by arranging all the data in ascending order.
- If you happen to have an odd number of data points, then select the middle value as your median.
- But if you have an even number of data points, select the 2 middle numbers, calculate the average, and the resulting value is your median.
As noted, the median is crucial, where outliers might distort the arithmetic mean. It can be applied when analyzing income data, property prices, or any skewed data distribution.
Real-Life Application
Here is a good example of income distribution:

Let’s say you have a company or a business with 5 employees, each earning different salaries:

Now let’s calculate the average salary (mean) each employee receives:
- Add the salaries:
3000 + 3500 + 4000 + 20000 + 4500=35000
2. To find the average salary, we will have to divide this number by the number of employees 5:
Average = 35000 / 5 = 7000
These calculations show that the average salary is $7,000, but does this accurately represent the average salary most employees get? The answer to that is NO, this is simply because there is an employee’s $20,000 salary. This alone is an outlier; therefore, we need to use the median to find the average salary:
So let’s do that:
- We start by arranging the salaries in ascending order:
3000, 3500, 4000, 4500, 20000.
- From there, we can now see that the middle salary is $4000, and that is the median, which accurately represents the average salary employees get paid.
What if you have to number in the middle, for example:
3000, 3500, 4000, 4300, 4500, 20000.
In this case, you’ll have to take the two middle salaries, which are $4000 and $4300 – Sum them up totaling to $8300. Now, let’s find the average to find the median.
Average = 8300 / 2 = 4150
When to use median?

Ideally, the median acts as a close substitute to the mean since it helps put outliers within a dataset under consideration. This means whatever you get as the average using the median is an actual representation of the entire dataset.
The median is applied in the following real-life scenarios:
- House prices: Real estate markets often use median home prices to represent the market better than average prices, which could be skewed by expensive properties.
- Income distributions: When comparing wages, especially in economies with large income inequality.
- Skewed distributions: The median is more useful for any dataset where the values are not equally distributed and not symmetric.
How to calculate the average percentage
As we go from numbers to percentages, averages are still required, more so when working with a large data set. Average percentage is used if you have a number of percentages that you would want to combine and come up with a single percentage.
This is very popular in grading systems, customer feedback, or organizational and business performance indicators.
Formula:
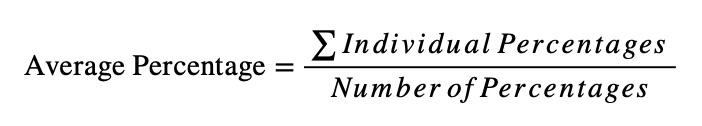
Example
To better explain, let us consider an example of a student’s performance. If a student has completed three courses, and their results in percentages are as follows: 78%, 85%, and 92%.
How did the student perform? To know the general performance, all the results obtained will be in percentage form and will be added together and divided by the total number of courses.
78 + 85 + 92 = 255%
Average Percentage = 255 % / 3 = 85
The student’s average percentage across all courses is 85%.
Related: Percentage calculator
How to calculate GPA (grade point average)
The Grade Point Average, also abbreviated as GPA, is a generalized tool that is employed in all education systems to evaluate the performance of a learner at the end of any given semester or academic year.
It is the average percentage from all courses that have credit points, which are awarded according to the grades students obtained for every course, for example, A=4.0, B=3.0.
Formula:
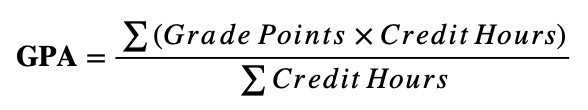
Now, let’s consider an example to make it comprehensible.
Let’s say a student successfully achieved the following grades and credit hours for three courses:
- Course 1: A (4.0) with 3 credit hours
- Course 2: B (3.0) with 4 credit hours
- Course 3: A (4.0) with 2 credit hours
To derive the GPA, you shall begin by multiplying grade points by the credit hours as applied to each course and then adding them all together. Following that, divide the total sum by the number of credit hours.
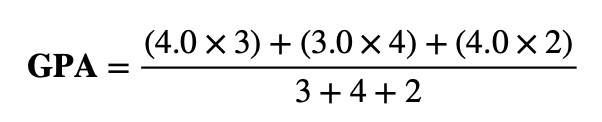
GPA = 32 / 9 = 3.56
And just like the GPA for that student is 3.56.
What is the importance of GPA?
- Academic Assessment and Achievement
GPA is used as an overall indicator of a student’s performance throughout his or her academic years. It enables an Institution to assess the performance of students and how prepared they are for another challenging course or being put on the Honors program.
- Scholarships, Grants, and Honors Scholarship and grant programs are open to students who meet the following requirements:
Besides, GPA is commonly a requirement for scholarships, financial aid, and academic Honors programs. It is used as a criterion for both financial assistance based on merit and recognition and academic achievements.
- Job Openings and Masters Programs
Compared with other measures, GPA is often applied to evaluate academic capabilities and preparedness for a graduate school or a professional position in an organization among employers and graduate schools. It is widely used as a benchmark for university admission and in competitive employment opportunities, particularly for young talents.
- Self-Assessment and Motivation
To students, GPA is an effective feedback mechanism in that it allows the student to assess performance in specific subjects or overall. It can make them develop a desire to work harder in some areas and also stay focused in their studying process.
How to Calculate Moving Averages?
When you want to track the progress over a specific time on a continuous basis, you can utilize the moving average.
With a moving average, you can easily smooth out fluctuations in data. This action helps to reveal trends over time, which is ideal for determining the overall progress of whatever is being measured. The best application of moving averages is in stock market analysis. In addition, it is still ideal for business forecasting and tracking long-term trends in any time-based data.
The formula for a simple moving average (SMA):
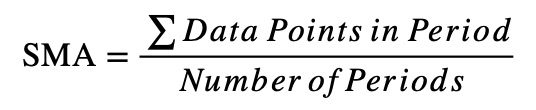
Here is a good Example:
Let’s assume that the stock price of company X has been steadily increasing over the last 5 days:
From $50, $52, $54, $53, and $55.
Now, to calculate and determine the 3-day moving average for the last three days:
Take the average of the first 3 days:
GPA = 50 + 52 + 54 / 3 = 52
2. Slide the window forward one day and calculate the next average:
GPA = 52 + 53 + 54 / 3 = 53
3. Continue sliding the window to find the next average:
GPA = 54 + 53 + 55 / 3 = 54
Moving averages are widely used by traders to identify upward or downward trends in stock prices.
How to Calculate Mode?
The mode in statistics refers to that number that repeats itself most frequently in a given set of data. This statistic is particularly useful when there is a need to identify the highest or most sold item, for example, the shoe size that is most sold in a given area, the highest grade achieved by the learner, or the number one product in the market.
Here are steps to calculate mode in a given dataset:
- Start by listing all data points.
- After that, find the value that occurs most frequently.
Example:
Let’s say you run a shoe store and manage to sell 10 pairs of shoes in a week with the following sizes: 7, 8, 8, 9, 7, 10, 8, 9, 7, 7. So, which shoe size is frequently bought?
Let’s do the count:

The model is size 7, which is the most commonly sold shoe size in the store.
How to Calculate Weighted Average?
The weighted average is applicable compared to the simple arithmetic mean in most cases when computing means where data points have varying significance. This is commonly used in the grading system, investment yield, and performance appraisal.
Formula:
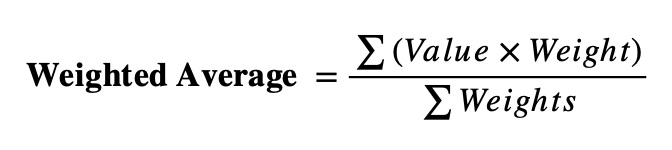
Here is an example:
In a course, a student’s final grade is based on the following assessments, each with a different weight:
- Homework: 85% (20% weight)
- Midterm: 78% (30% weight)
- Final Exam: 90% (50% weight)
To calculate the weighted average:
- Multiply each score by its weight:
(85×0.2) + (78×0.3) + (90×0.5) = 17 + 23.4 + 45 = 85.4
The student’s final weighted average score is 85.4%.
When to Use Harmonic Mean?
The harmonic average is applied in scenarios where the data concerns a certain ratio, especially speed, efficiency, cost, per unit, and so on. It serves as a better means in cases of ratios and rates, which is why it is widely used in physics, economics, and finance.
Formula:
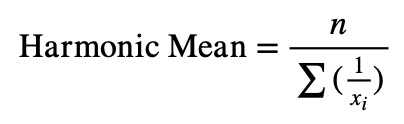
Where n is the number of values, and Represents the individual data points.
Example:
Suppose that the velocity of a vehicle in a distance of the first half of a certain path is 60 km/h, whereas in the second half the velocity is 90 km/h. In this case, what is the average speed for the entire journey?
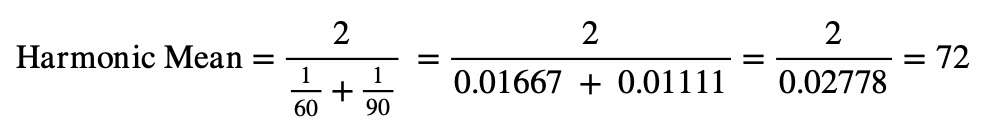
Now, 72 km/h is the average speed of the entire journey, not 75 km/h, which you get when you use simple arithmetic average calculations.
Final Thoughts
Learning how to calculate averages is a fundamental and crucial basis of data analysis, from which many decisions are made, both on the academic and professional front.
Averages reduce a dataset containing complex information to one number representing it; therefore, it makes the interpretation of trends, comparisons, and derivation of a conclusion quite easier to handle.
Averages are not limited only to the process of averaging; they have a great chance of being used in real life. For instance, in education, it is used to calculate the GPA that defines the performance of a student, resulting in scholarships or getting into certain programs.
In financial and business fields, it is used for the examination and analysis of investment returns or the trends of the markets, and of course, sales performance analysis is strictly used to predict future growth.